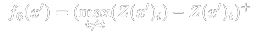终于是把这玩意儿自己实现了一遍,恰逢miniL CTF,这文章虽然是22.04.09写的,但是估计博客得等到五月多才会更新,届时将也再补充一些在miniL CTF中本题的情况
L2 Targeted Attack
前置知识:全连接神经网络
参考文献:Towards Evaluating the Robustness
碎碎念:这段时间又在捣鼓Uncertainty ,加点内容想去参加吉比特的Jam,等Jam完了可能的研究对象应该是CNN,UE5之类的(神经细胞自动机暂时就先鸽了,但确实很有趣,以后应该回去看看的
miniL CTF
有幸在校内的miniL CTF出一次题(一个L2TargetedAttack,一个CheatEngine改坐标),本来想做一个CNN的L2 Targeted Attack,这样可以把情景包装得有趣一些,但是还是太懒了,弄完这个就不想弄CNN了,就先出到这里了
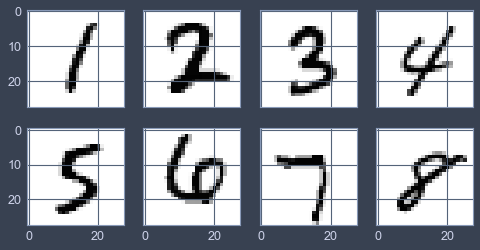
题目名为NEXT,顾名思义就是让你对MNIST中的几个Samples加扰动,使得如下的8个Samples被模型识别成其原本lable的下一个数,如1→2,2→3...
为了让题目有个情景,所以把原本的weight给轮了一下顺序,原lable本应是[0,1,2,3,4,5,6,7,8,9],被改成了[1,2,3,4,5,6,7,8,9,0],于是乎题目就有了一个虽然不合理但可以忽悠人的情景
模型为带DropOut的FCNN,虽然带DropOut,但是整体梯度比较明显,对扰动的鲁棒性欠佳,很适合作为攻击对象
源码上对原本的函数做了一点混淆,比如softMax缩写成SM之类的,主要是为了选手深入了解神经网络之后再入手题目,不要底层没摸清楚做纯纯的TFboy
限制了L2和Linf的大小,是为了让做题人明确这是一个L2 Attack
task中不包含torch,TF之类的,但可以把weight手动导入一下,然后使用如tf.gradientTape之类的方法自动求梯度,我自己解是用比较土的手搓BackProp
下载题目及exp
以下是题目代码
task.py
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 import pandas as pdimport numpy as npfrom secret import flagL2CONSTRAIN = 5.6789 LINFCONSTRAIN = 1.234 CONFIDENCE = 0.8 def RL (x ): return np.maximum(x, 0 ) def SM (x ): return np.array(np.exp(x) / np.sum (np.exp(x), axis=1 )) def AB (x ): x = np.matrix(x) return np.c_[np.ones((x.shape[0 ], 1 )), x] class ANN : def __init__ (self, uNum ): self.uNum = uNum self.lNum = len (uNum) self.w = [0 ] self.Z = [0 ] self.A = [0 ] def FP (self ): for i in range (1 , self.lNum - 1 ): self.Z.append(AB(self.A[-1 ]) * self.w[i]) self.A.append(RL(self.Z[-1 ])) self.Z.append(AB(self.A[-1 ]) * self.w[-1 ]) self.A.append(SM(self.Z[-1 ])) def PRED (self, x ): self.Z[0 ] = np.matrix(x) self.A[0 ] = np.matrix(x) self.FP() return np.array(self.A[-1 ]) def LOAD (self, fileName ): f = open (fileName, "rb" ) wt = np.frombuffer(f.read(), np.float64) f.close() for i in range (1 , len (self.uNum)): data = wt[: (self.uNum[i - 1 ] + 1 ) * self.uNum[i]] shape = (self.uNum[i - 1 ] + 1 , self.uNum[i]) self.w.append(np.matrix(data).reshape(shape)) wt = wt[(self.uNum[i - 1 ] + 1 ) * self.uNum[i]:] def CHECK (mask: np.matrix, myNN: ANN, x ): l2 = np.sum (np.linalg.norm(np.array(mask), axis=1 )) / 8 linf = np.max (np.linalg.norm(np.array(mask), ord =np.inf, axis=1 )) if l2 > L2CONSTRAIN: print("Huge L2 " + str (l2)) return if linf > LINFCONSTRAIN: print("Huge Linf" + str (linf)) return res = myNN.PRED(x + mask) for i in range (8 ): lable = np.argmax(res[i]) if lable != i + 1 : print("Wrong Lable " + str (lable) + ", " + str (i + 1 )) return if res[i][lable] < CONFIDENCE: print("Unconfident " + str (lable) + ", " + str (i + 1 ) + ", " + str (res[i][lable])) return print(flag) if __name__ == '__main__' : uNum = [784 , 512 , 256 , 10 ] myNN = ANN(uNum) myNN.LOAD("weight.dat" ) data = pd.read_csv(r'picData.csv' ) x = np.matrix(data.iloc[:, 1 :]) mask = [] for i in range (8 ): print(">> Mask " + str (i + 1 ) + " :" ) maskTemp = [] for j in range (784 ): maskTemp.append(float (input ())) mask.append(np.array(maskTemp, dtype=np.float64).ravel()) mask = np.matrix(mask) CHECK(mask, myNN, x)
Attack
Loss
参考论文,在Loss中包含了对L2的惩罚项,我implement的时候使用的是类似于参数正则化一样的方法,简单但有效,在每次迭代后:根据对L2的限制,让最终的噪声Pert自减一点点
而对于如何在Loss中体现出逼近Target,直接借鉴一下Carlini大神的结论,即参考文献中的f6,毕竟这些东西就是凭经验凭感觉弄出来的,他们基本也就是选了一些自己觉得有可能可行的Loss然后全部跑一遍,找一个效果最好的
其中加号上标表示对括号内的参数x执行max(x, 0)
大概意会一下,首先这玩意儿得从logits层开始回归,然后至于他这个Loss的思想也就字面意思:打压当前概率最高的,同时扶持target的概率
我没有完全按照他的loss来(主要是为了方便),但是思想都是一样的,我implement的就是一个对无关项置零的交叉熵,代码如下
1 2 3 4 5 6 7 def d_crossEntPert (self ): mat = np.matrix(self.A[-1 ] - self.y) if np.argmax(np.array(self.y).ravel()) != np.argmax(np.array(self.A[-1 ]).ravel()): for i in range (10 ): if i != np.argmax(np.array(self.y).ravel()) and i != np.argmax(np.array(self.A[-1 ]).ravel()): mat[0 , i] = 0 return mat
注1:此处的Loss还并非最终形态,因为没有加入对Pert的惩罚项
注2:关于为什么要在最终label是target的情况下直接return,则是因为这样在已经找到属于target的决策区域后的下降速度更快,还可以防止梯度消失
Get Gradient
由于是自己搓的FCNN,获取梯度直接backProp就行了,比如想要倒数第二层的dZ,backProp之后就直接FCNN.dZ[-2],非常方便,这个手搓BP的梯度也拿去和tensorflow中的gradientTape求出的梯度做了对比,保证梯度正确
简化剔除了一些常规BP在此情境下不需要的内容,得到以下代码
1 2 3 4 5 6 7 8 9 10 11 12 13 def backProp (self, d_lossFunc ): self.dZ[-1 ] = d_lossFunc() dw = self.A[-2 ].T * self.dZ[-1 ] db = np.sum (self.dZ[-1 ], axis=0 ) self.dw[-1 ] = np.r_[db, dw] for i in reversed (range (1 , self.layerNum - 1 )): self.dA[i] = RemoveBias(self.dZ[i + 1 ] * self.w[i + 1 ].T) self.dZ[i] = np.multiply(d_relu(self.Z[i]), self.dA[i]) dw = self.A[i - 1 ].T * self.dZ[i] db = np.sum (self.dZ[i], axis=0 ) self.dw[i] = np.r_[db, dw] self.dA[0 ] = RemoveBias(self.dZ[1 ] * self.w[1 ].T) self.dZ[0 ] = self.dA[0 ]
Fool
现在关键成分都已经齐全了,就可以开始生成AdversarialPerturbation了
基本的迭代过程大致如下:
把target设置成y,因为loss函数中会用到(比如要把6糊弄成7,则target=7)
ForwardProp()
判断target的confidence是否符合要求,符合则return,不符合则继续
BackProp()
对梯度加入关于Pert的惩罚项
在此基础上,还进行了几点优化:
因为这个方法肉眼可见的容易出现惩罚项与逼近Target的方向相反的情况,所以加入了一个在Stuck时进行随机扰动的功能
对起点进行比较小的随机扰动,稍微差异化每次下降过程
(在输出中加emoji主要是为了快速浏览运行结果,而且事实证明Jupyter对此支持是没问题的,看着很直观
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 class Fool : def __init__ (self, myNetwork ): self.Network = myNetwork def GetGrad (self, X ): pred = self.Network.predict(X) self.Network.backProp(self.Network.d_crossEntPert) return self.Network.dA[0 ], pred.ravel() def Fool (self, X, y, tar, foolRate=0.5 , maxIter=500 , step=0.05 , minGrad=0.05 , maxGrad=10 , constrain=10 , stuckRandL2=1 , initRandL2=1 ): rand = np.matrix(np.random.randn(1 , 784 )) pert = np.zeros((1 , 784 )) + initRandL2 * rand / np.linalg.norm(rand) loss = [] L2Rec = [] cnt = 0 stuckCnt = 0 stuckJudgeCnt = 0 success = False self.Network.predict(X + pert) print("init: " + str (y) + " prob: " + str (self.Network.A[-1 ].ravel()[y])) self.Network.y = OneHot( 1 , self.Network.unitNum[-1 ], y) if tar == -1 else OneHot(1 , self.Network.unitNum[-1 ], tar) while (True ): print("\rcnt: " + str (cnt) + " stuck: " + str (stuckCnt), end='' ) grad, pred = self.GetGrad(X + pert) loss.append(np.linalg.norm(self.Network.A[-1 ]) if tar == -1 else -np.sum (np.array(self.Network.y) * np.log(self.Network.A[-1 ]) + np.array(1 - self.Network.y) * np.log(1 - self.Network.A[-1 ]))) if ((self.Network.A[-1 ].ravel()[y] < foolRate if tar == -1 else self.Network.A[-1 ].ravel()[tar] > foolRate) and stuckJudgeCnt > 5 ): print("\n⭕ OK: " + str (np.argmax(pred)) + " " + str (self.Network.A[-1 ].ravel()[np.argmax(pred)]) + "\n" ) success = True break if np.linalg.norm(pert): para = max ((np.linalg.norm(pert) - constrain) ** 3 , 0 ) grad -= np.sum (np.array(pert) * np.array(grad)) * \ (pert / np.linalg.norm(pert)) * para L2 = np.linalg.norm(grad) L2Rec.append(np.array(L2).ravel()) if L2 > maxGrad: grad *= maxGrad / L2 if L2 < minGrad: if L2 == 0 : print("\nERR: grad is zero" ) break grad *= minGrad / L2 pert -= grad * step cnt += 1 if cnt == maxIter - 1 : print("\n❌ nope: " + str (y if tar == -1 else tar) + " " + str (self.Network.A[-1 ].ravel()[y if tar == -1 else tar]) + "\n" ) break if cnt > 1 and abs (loss[-1 ] - loss[-2 ]) < 0.1 : stuckJudgeCnt += 1 if stuckJudgeCnt > 10 : rand = np.matrix(np.random.randn( pert.shape[0 ], pert.shape[1 ])) pert += rand / np.linalg.norm(rand) * stuckRandL2 stuckJudgeCnt = 0 stuckCnt += 1 return success, pert, loss, L2Rec
Exp
于是我们只需要基于以上的基础再对每个数字计算一遍即可
考虑到要使得L2尽可能小,我使用动态的Constrain,使得搜索结果的L2快速减小到一个可观的范围
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 import pandas as pdimport numpy as npimport KyNetExpX = np.matrix(pd.read_csv(r'picData.csv' ).iloc[:, 1 :]) unitNum = [784 , 512 , 256 , 10 ] FCNN = KyNetExp.Network() FCNN.Init(unitNum) FCNN.LoadParameters("weight.dat" ) Fool = KyNetExp.Fool(FCNN) pert = [] deltaConstrain = 0.1 maxUnsuccessCnt = 10 for i in range (8 ): print("\n-------------------- " + str (i + 1 ) + " --------------------\n" ) bestPert = np.matrix(np.ones((1 ,784 )) * np.inf) constrain = 30 UnsuccessCnt = 0 while (UnsuccessCnt < maxUnsuccessCnt): success = False success, pert_i, loss, L2Rec = Fool.Fool(X[i], i+1 , i+2 , maxIter=500 , foolRate=0.8 , constrain=constrain, stuckRandL2=1 , initRandL2=1 , minGrad=0.001 ) if success: if np.linalg.norm(pert_i) < np.linalg.norm(bestPert): constrain = min (np.linalg.norm(pert_i) - deltaConstrain, constrain) bestPert = pert_i UnsuccessCnt = 0 print("----------------------------------" ) print("# New Constrain: " + str (constrain)) print("----------------------------------\n" ) constrain -= deltaConstrain / 2 else : UnsuccessCnt += 1 pert.append(bestPert)
最终生成的Pert数据如下
1 2 3 4 5 6 7 8 9 10 11 12 13 np.linalg.norm(np.array([np.array(i).ravel() for i in pert]), axis=1 ) >> array([4.09481434 , 4.2946097 , 6.64396102 , 5.90332629 , 6.05583615 , 5.71162228 , 6.26226203 , 3.06447416 ]) np.sum (np.linalg.norm(np.array([np.array(i).ravel() for i in pert]), axis=1 )) / 8 >> 5.2538632468131485 np.linalg.norm(np.array([np.array(i).ravel() for i in pert]), ord =np.inf, axis=1 ) >> array([0.51915417 , 0.6969855 , 0.94458608 , 0.8020708 , 0.99483219 , 0.70698208 , 1.12368025 , 0.41853863 ])
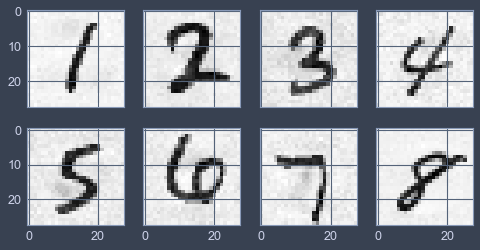
宏观感受如下
对比Carlini的论文中的L2数据,我认为这样的结果勉强可以接受,但鉴于视觉效果仍然不佳,之后可能会考虑在更大规模的model和dataset上做adversarial attack方面的种种实验
DumbAss
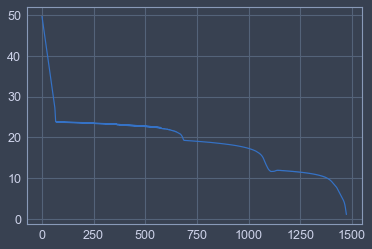
一开始还想着靠单纯的梯度下降直接,硬着提高target的自信度,但是导致的问题就是各种梯度消失梯度过缓之类的,比如我当时的loss是这样下降的
具体是把6识别成7的情景,范数如下,吃力不讨好了属于是
1 2 L2 : 8.161735079209715 Linf: 1.188402119264267
在做这个L2 Targeted Attack的时候,最多的时间应该是浪费在以下这几件事上:
float64与float32在加载与储存的时候没有注意类型,导致不能及时与tensorFlow对答案softMax偏导的函数错误,导致最终偏导错误文献查找,找到Carlini的这篇文章花了挺多时间的